Signe d’une dérivée et sens de variation
Niveau de cet exercice : 
Énoncé
La courbe ci-dessous représente une fonction définie et dérivable sur l’intervalle
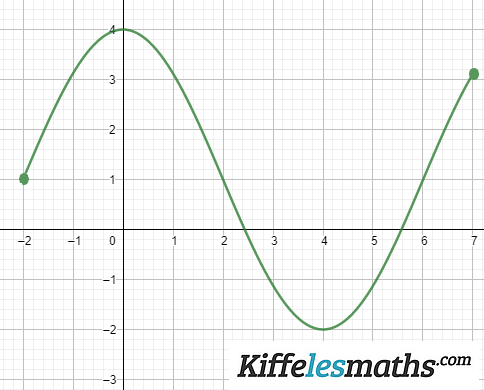
1- Par lecture graphique, déterminer le sens de variation de sur
et déduire, le signe de
sur
.
Correction
est croissante sur
et sur
donc
est positive.
est décroissante sur
donc
est négative.
Niveau de cet exercice : 
Énoncé
soit est une fonction définie sur
, Le tableau ci-dessous donne le signe de
sur
.
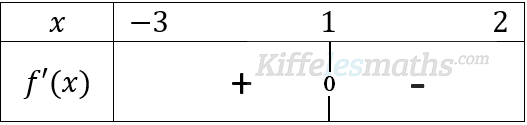
Dresser le tableau de variations de sur
.
Correction
Sur l’intervalle on a
alors
est croissante.
Sur l’intervalle on a
alors
est décroissante.
donc
Niveau de cet exercice : 
Énoncé
Soit la fonction définie sur
par
.
1- Calculer .
2- Déduire les variations de sur
.
Correction
1- est une fonction polynôme donc elle est dérivable sur
.
2-
donc est croissante sur
.
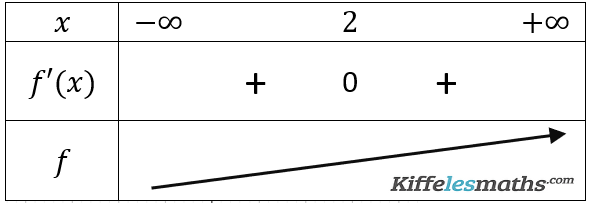
Tableau de variation de .
Niveau de cet exercice : 
Énoncé
soit est une fonction définie sur
,
Le tableau ci-dessous donne le signe de et la variation de
sur
.

Est que admet des extremum ?
Correction
D’après le tableau, s’annule en
en changeant de signe donc
alors
est un extremum, et puisque
sur
donc est un maximum local de
au voisinage de
.

