Equation de la tangente a une courbe
Niveau de cet exercice : 
Énoncé
Soit la fonction définie sur
par
et
sa courbe dans un repère du plan.
1- Calculer .
2. Montrer que est dérivable en
et déterminer
.
3- Donner l’équation de la tangente de
en
.
4- Vérifier les résultats obtenus en traçant en utilisant GeoGebra.
Correction
1-
et
alors
2-
On a
donc est dérivable en
et on a
.
3- Équation de :
est dérivable en
donc
admet une tangente en
équation :
c’st à dire
donc
4-
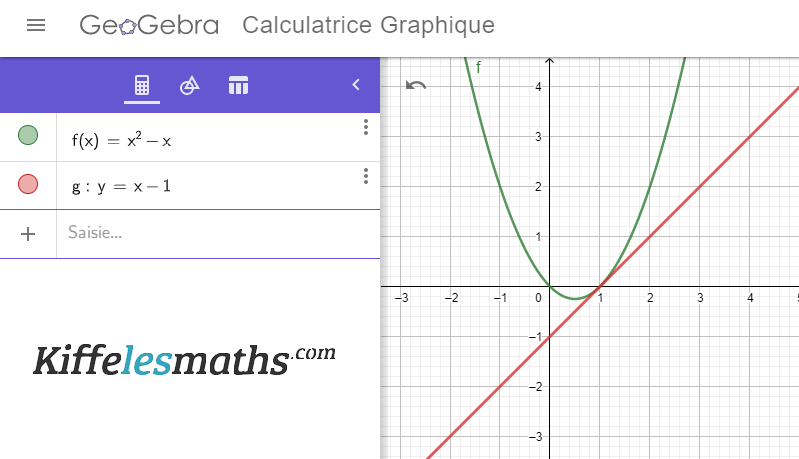
Niveau de cet exercice : 
Énoncé
Soit la fonction définie sur
par
et
sa courbe dans un repère du plan.
1- Calculer .
2. Montrer que est dérivable en
et déterminer l’équation de
la tangente de
en
.
Correction
1-
On a et
donc
2-
On a
alors est dérivable en
et
, or
admet une tangente
en
d’équation
donc
Finalement : .
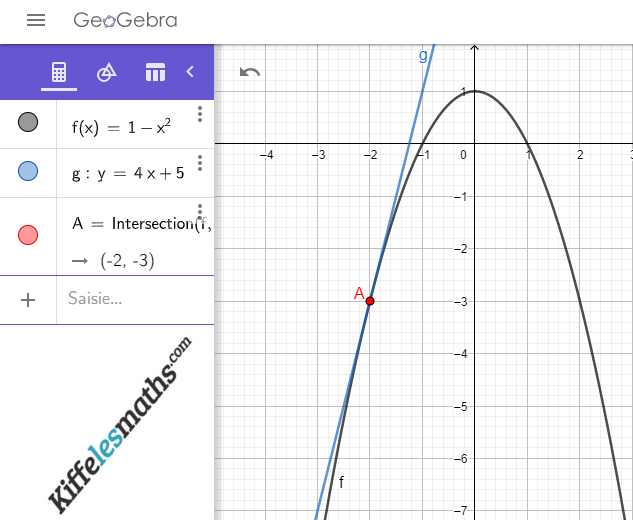
Niveau de cet exercice : 
Énoncé
Soit la fonction définie par ça courbe ci-dessous courbe ci-dessous, et
est la tangente de
en
.
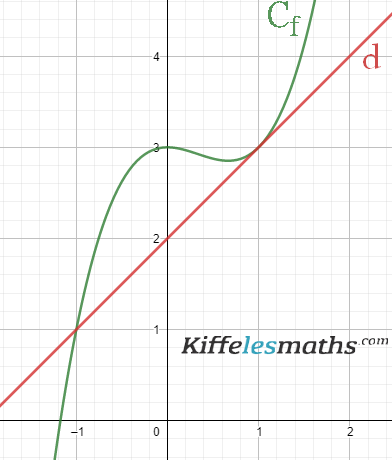
Déterminer graphiquement .
Correction
Graphiquement, est le coefficient directeur de
, ,
a partir de la courbe on a sont deux points de
alors
.

