SYMETRIE AXIALE – Série d’exercices 01
Niveau de cet exercice : 
Énoncé
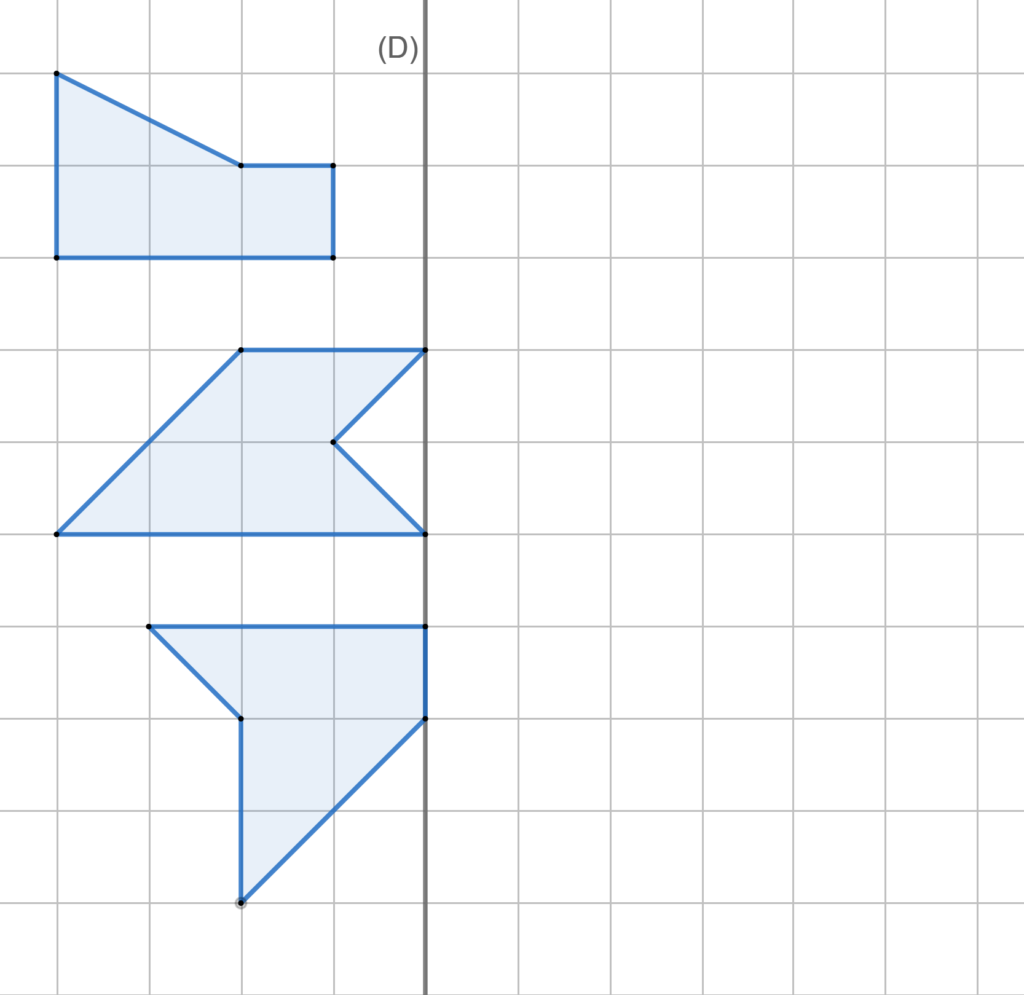
Trace le symétrique de chacune des figures ci-dessous par rapport à la droite indiquées :
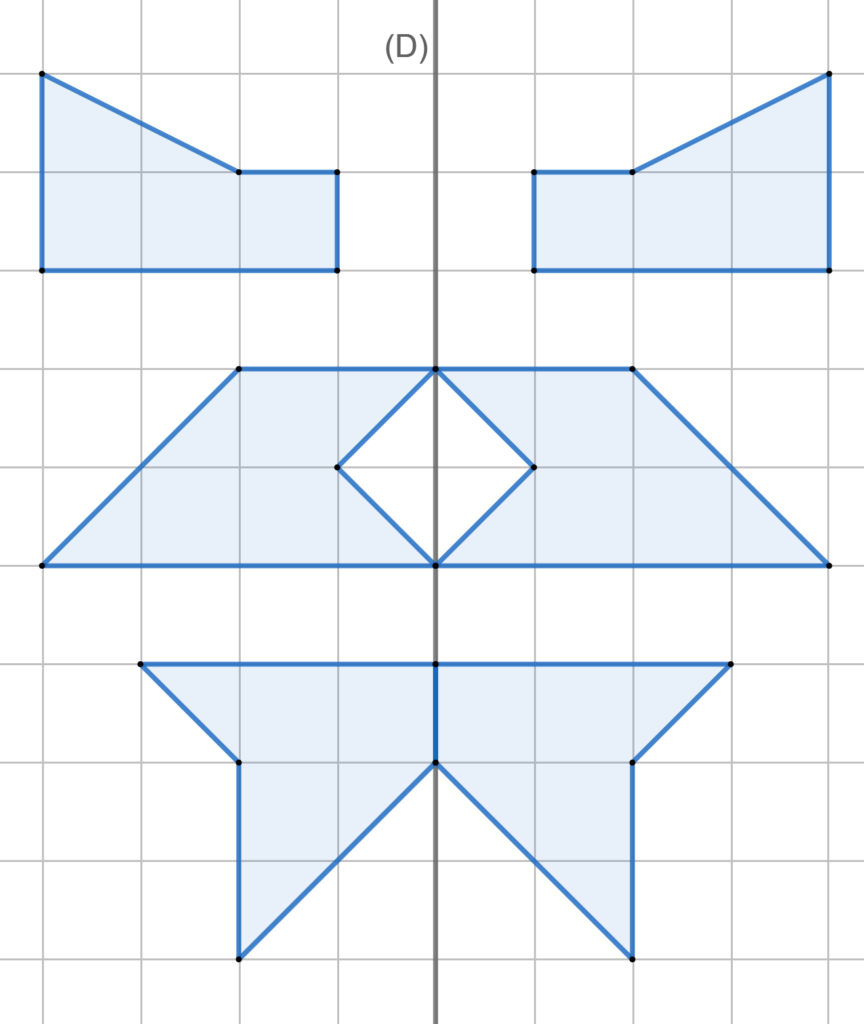
Correction
Niveau de cet exercice : 
Énoncé
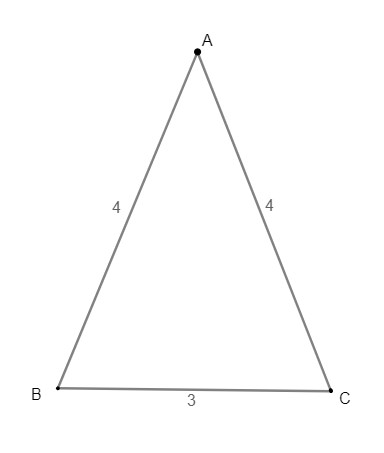
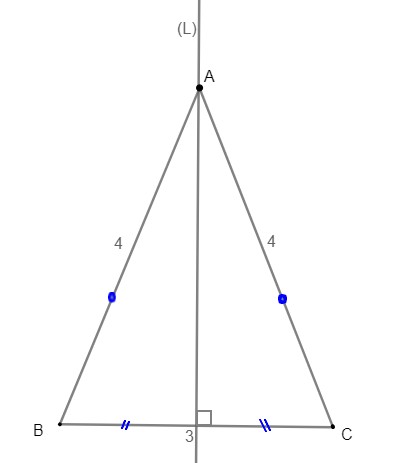
un triangle isocèle en
tel que
et
1- Construire le triangle .
2- Construire la médiatrice du segment
.
3- Quel est le symétrique de par rapport à
.
4- Quel est le symétrique du segment par rapport à
.
5- Quel est le symétrique de la droite par rapport à
.
6- Quel est le symétrique du triangle par rapport à
.
Correction
un triangle isocèle en
tel que
et
1-
2- la médiatrice du segment
.
3- Le symétrique de par rapport à
est
4- Le symétrique du segment par rapport à
est le segment
5- Le symétrique de la droite par rapport à
est la droite
lui même.
6- Le symétrique du triangle par rapport à
est
lui même.
Niveau de cet exercice : 
Énoncé
Tracer les axes de symétrie des lettres suivantes :

Correction

Niveau de cet exercice :
Énoncé
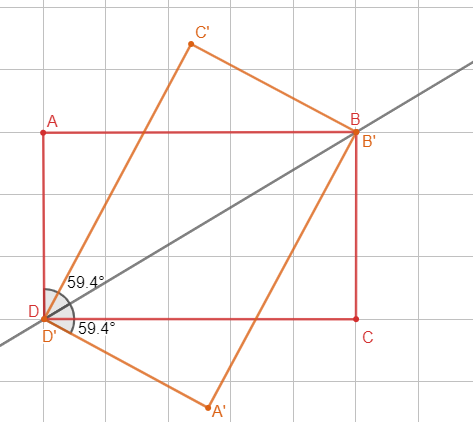
un rectangle tel que tels que
et
1- Construire le symétrique du rectangle
par rapport à la droite
2- Quel est le symétrique de l’angle .
3- Comparer les deux angles et
.
Correction
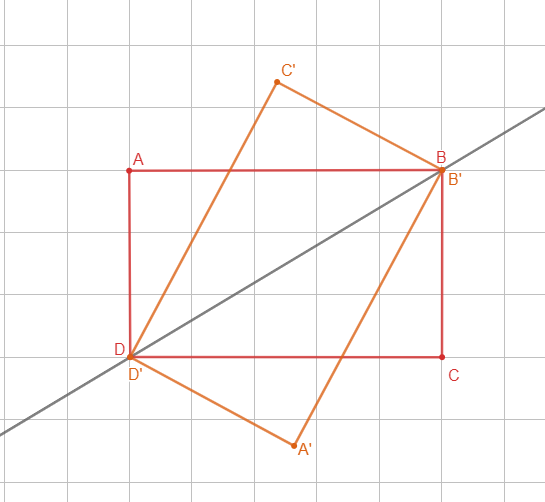
1- Soient et
les symétrique successives de
et
par rapport à la droite
, alors le symétrique du rectangle
est le rectangle
2- le symétrique de l’angle .
Le symétrique de par rapport à la droite (D) est
Le symétrique de par rapport à la droite (D) est
lui même
Le symétrique de par rapport à la droite (D) est
lui même
donc le symétrique de l’angle par rapport à la droite (D) est l’angle
3- Comparons les deux angles et
.
Le symétrique de par rapport à la droite (D) est
Le symétrique de par rapport à la droite (D) est
lui même
Le symétrique de par rapport à la droite (D) est
lui même
alors le symétrique de l’angle par rapport à la droite (D) est l’angle
donc